The HLM Proof Assistant

All definitions and theorems are shown in a tree on the left side of the main window. Theorems and different kinds of definitions are distinguished by their icons. For theorems without a well-known name, the statement is shown in an abbreviated form. Moving the mouse over an item displays the actual definition or statement.

The tree can be used to search for one or more keywords; the search result acts as a filter.

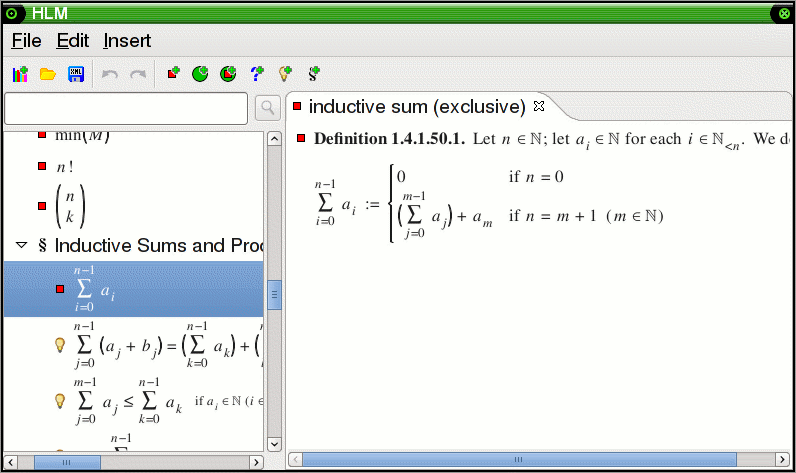
The strongest point of HLM is probably the user's ability to attach a custom notation to each definition. In combination with support for bound variables, many concepts can be displayed in a familiar way. This notation is even used in the tree, eliminating the need to remember names. Here is the definition of a generalized sum of natural numbers:

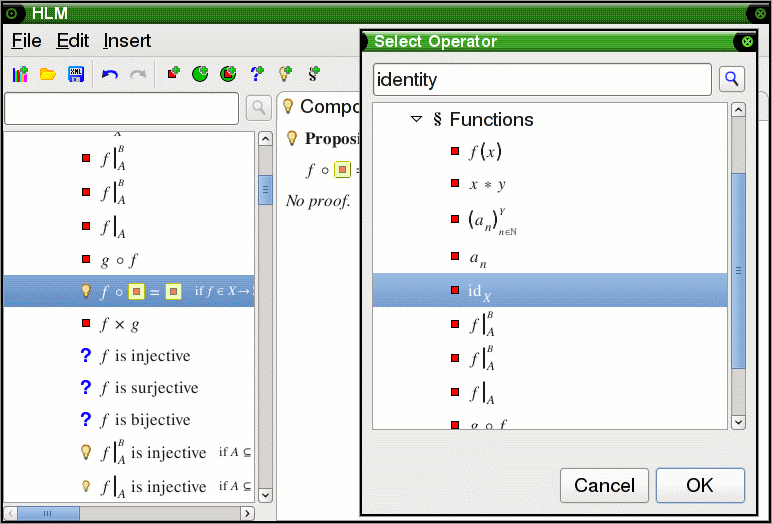
Instead of typing names and symbols, the user selects everything from menus. This is the menu for entering a formula, which includes a list of most-recently used applicable definitions:

In order to optimize the contents of the list of most-recently used definitions, a type system ensures that all entries are meaningful. In the following screenshot, the system expects a function, and also figures out that its codomain must be X, even though functions are not built-in but defined in the library.

If the needed definition is not in the list of most-recently used items, clicking on "Operator..." brings up a dialog with an appropriately filtered tree. Alternatively, one can use drag&drop from the tree on the left.

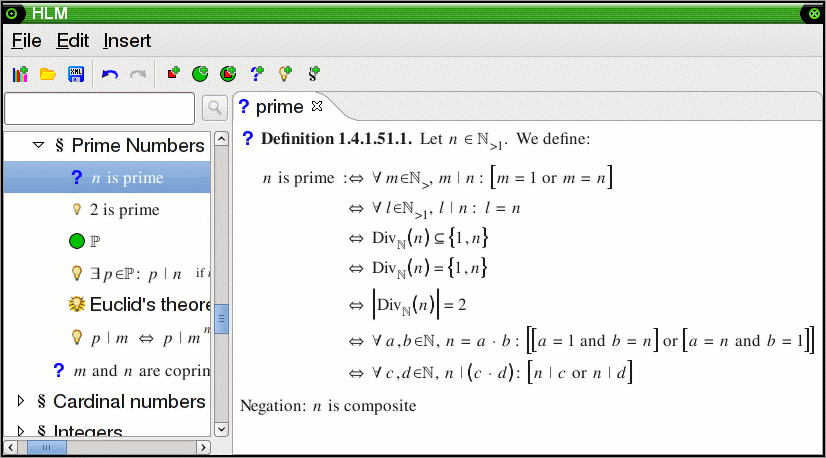
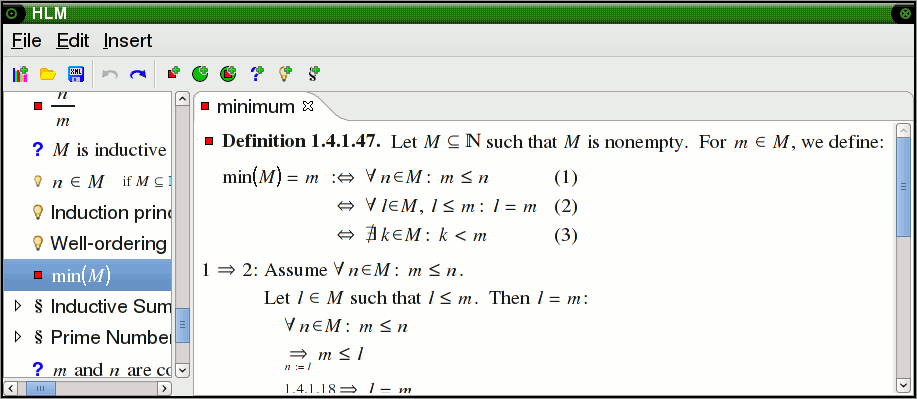
This is what a finished definition looks like. If multiple equivalent formulations exist, they can be entered together, so the library becomes less cluttered and proofs become shorter. Note that the different definitions for "being prime" are equivalent only if n>1, which is specified as a constraint that must be satisfied before the definition can even be used.

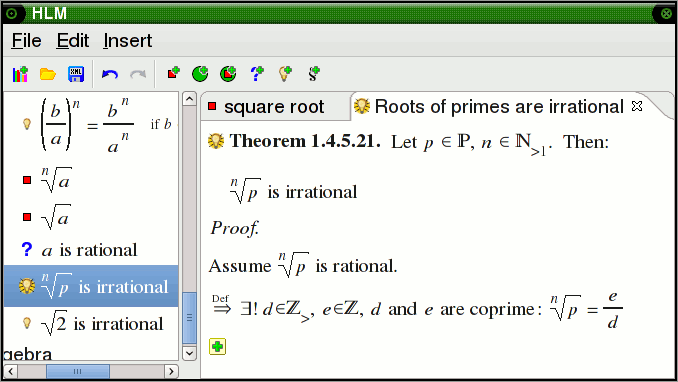
Another mathematical feature, special support for implicit definitions:

Existing sets can be embedded into newly constructed sets. The type system ensures that no ambiguities can arise.

Proofs are entered by selecting steps from menus. For example, if an object has multiple equivalent definitions, it can be rewritten into any of them:

Selecting a proof step from the menu inserts it into the proof. Here is the result of the previous screenshot:

Finally, this is what a finished proof looks like.
Everywhere in HLM, moving the mouse over a symbol shows its definition, and clicking opens it.